dsa个人题库
本文是作者在复习数据结构刷题的时候遇到的简单但不完全简单的小题(大题的话博主已经弃疗了…要杀要刮随邓公了)。dsa知识点相当的多,随便举一些例子吧:主定理、动态规划、向量列表、先序遍历的递归/迭代版、AVL树和红黑树、散列冲突、dijkstra、堆合并、KMP算法、各种各样的排序(以及它们的性质和改进)…
其实重点就是红黑树这些复杂结构的理解,只要这些知识学会了就行。反正难题不会,会题不难,不是吗?
总之,这些题目是巩固理解、记牢算法的好选择,而难度较大的证明大题则超出了博主的理解范围…
对于二分查找版本C,当查找区间的长度缩小为0时,V[lo]是:
min{0 < r < n & e < V[r]}。因为事实上命中的秩是lo-1,而lo-1右边的(也就是从lo开始的左闭右开区间)都是严格大于e的元素。故而V[lo]是大于e的,而v[lo-1]不大于e。顺便一提,课本中的向量中的lo和hi永远是左闭右开区间,即[lo,hi)。
在有序向量V中插入元素e并使之保持有序,下列代码正确的是:
V.insert( V.Search(e)+1 , e )。V.Search(e)应当+1,否则会将最后一个元素挤掉。
【这道题似乎是oop的题,可以无视它】是否可以将视频里向量扩容代码中的:
for (int i = 0; i < _size; i++) _elem[i] = oldElem[i];
替代为:
memcpy(_elem, oldElem, _size * sizeof(T));
不可以,与T的数据类型有关。简单地说,假如T不是基本数据类型例如string或一个类,那么=号或许是重载过的,前者相当于深拷贝;而memcpy是浅拷贝 (假如你去查memcpy的源代码的话会发现它就是在逐字节地复制hhhh),析构的时候可能会报错!
以递归的方式计算fib(n)的时间复杂度是Θ(2^n)?
错,实际上时间复杂度是Θ(1.618^n),故而只能说是O(2^n)而非θ(2^n)。
在向量V={2, 3, 5, 7, 11, 13, 17, 19, 23}中用插值查找搜索元素7,猜测的轴点mi为:
答案为1。 mi=lo+(hi-lo)*(e-V[lo])/(V[hi]-V[lo])
长度为n的列表,被等分为n/k段,每段长度为k,不同段之间的元素不存在逆序。对该列表进行插入排序的最坏时间复杂度为:
O(n*k)。插入排序的时间复杂度=O(n+I),其中I为逆序对(不是相邻逆序对)的数量。本题中最多有 n / k * k^2= n * k个逆序对。
顺便一提,逆序对与插入排序相关,而循环节与选择排序相关(循环节的数量决定了选择排序中“无效交换”的次数,期望为θ(log n) )。
(在中缀表达式求值中)什么时候进行实际的运算?
当前的操作符比栈顶的操作符优先级低时,即栈顶运算符优先级高时。因为每次运算都是对于栈顶运算符的运算。
在一棵树中,顶点p是顶点v的父亲,则它们的高度的关系是否为height(v)=height(p)-1?
不一定,比如p的左孩子是v,右孩子有一棵很大的子树,此时height(v)=0而height(p)=k。故而只能说height(v)<height(p)。
对以下二叉树进行先序遍历,刚访问完节点d时(迭代实现2)栈中的元素从栈顶到栈底依次为:
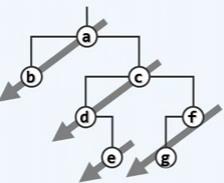
只有f。
事实上,“沿藤爬取”算法会先访问该节点,再将该节点的右孩子推入栈,并顺左侧藤下行。主算法会试图对每次调用“沿藤爬取”算法,并在无法继续爬取后将栈顶pop掉,再次对该元素进行爬取。
故而首先对a爬取,访问a,将c压栈,再访问b。此时“沿藤爬取”算法结束,将c pop掉并沿c爬取,访问c,将f压栈,再访问d,再将e压栈。故而刚访问完d的时候栈中只有c的右孩子f。
对以下二叉树进行中序遍历,节点c刚被访问完毕时栈中的元素从栈顶到栈底为:
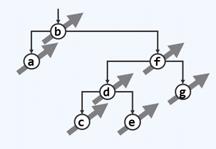
d和f。
中序遍历时,“沿藤爬取”算法会将每个节点入栈,直到爬完为止。回到主算法,算法会pop掉栈顶元素并访问它,同时试图进入它的右孩子。若有右孩子,则以右孩子为根实施“沿藤爬取”算法,若没有右孩子,则会再pop掉栈顶元素,以此为根实施“沿藤爬取”算法。
故而首先对b爬取,b入栈,a入栈,访问a,访问b,并且转向其右孩子f,对f进行爬取会将f,d,c入栈,访问c。
对以下二叉树进行层次遍历,节点F正欲出队时队列中的元素从队头到队尾为:
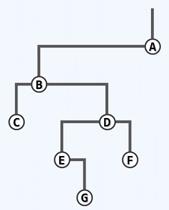
f和g。
请注意,层次遍历使用的辅助数据结构不是栈,而是队列。也没有藤算法,只有一个主算法。主算法会将根入队,并且每次循环将队首出队并访问,并将其左孩子入队、右孩子入队。
访问A,将B入队。访问B,将C和D依次入队…本算法比先序中序容易很多。
从n个节点的二叉树的叶节点u逐个节点地上溯到根节点的过程中,最坏时间复杂度为O(n)?
正确,因为极端退化的二叉树就是链表(即所有节点都只有一个孩子),BST也是一样的。
AVL树插入节点最多会使多少节点失衡?删除节点呢?
O(log n)和O(1)。事实上,删除节点至多只会令一个节点失衡
值得一提的是,插入节点后失衡的节点最低为其祖父(爷爷),而删除节点后失衡的节点最低可以是其父亲。但在调整时,插入导致的失衡只需一次单旋/双旋即可,而删除导致的失衡却可能需要至多O(log n)次单旋/双旋。
AVL树中删除节点引发失衡,经旋转调整后重新平衡,此时包含节点g,p,v的子树高度?
有可能不变也有可能减小1。请注意这里的子树高度是相比于原AVL树而言,即删除操作之前的树。如果子树高度不变,那么全树复衡;高度减1,则需要向上继续旋转。
顺便一说,插入节点后旋转,其子树高度一定不变,这也对应了上一个问题中所说的,插入后只需一次单旋/双旋。
伸展树采用双层伸展策略,即可避免最坏情况的发生?
错误。【这道题有点文字游戏…】只能减小最坏情况的频率,也就是最坏情况不致持续发生,但仍可能极少地发生。
如果说访问一次内存需要1秒,则一次外存访问大概需要:
一天。访问内存需要100 ns,而磁盘访问需要10^7 ns。两者相差10^5倍。
教材P 802的重散列(rehash)一定是扩容操作吗?
不一定。如果懒惰删除的标记太多,那么4 N(其中N是当前真实的非空桶,不包括懒惰删除标记)不一定比当前散列表的长度大,此时的重散列反而是缩容操作。这也是为什么我们不用2 M(M是散列表长度)而用4 N的原因。
红黑树在每次插入/删除操作后,拓扑结构的变化不超过O(1)。
正确。事实上,这是红黑树非常重要的性质之一。而AVL树虽然插入操作满足题意,但正如14题所说,删除操作可能会有O(log n)级别的拓扑改变。
当叔父节点u为红色时,修正双红缺陷导致的红黑树拓扑结构的变化为:
没有变化。RR1(叔父为黑)会改变O(1)的拓扑结构,但会立刻终止修正;而RR2(叔父为红)不会改变任何拓扑结构(而仅仅是将颜色重染),但可能会向上传递双红缺陷。
另一方面,对于删除操作,对于叔父节点、叔父节点的孩子、祖父的颜色共有四种情况,其中BB-1、BB-2R都是一蹴而就的,BB-3是两蹴而就的,只有BB-2B(叔父节点为黑、叔父节点的孩子均为黑、祖父为黑)的情况可能向上传递双黑缺陷;但只有BB-1和BB-3会改变拓扑结构,故而跟如20题所说,红黑树的插入、删除操作都不会使拓扑结构改变较大。
伸展树单次查找操作的最坏时间复杂度比AVL树大。
正确。在单链伸展树中插入叶子元素,需要一直向上双层伸展(事实上双层伸展也是“逐层”伸展,只是顺序略有不同),此时复杂度为O(n)。
值得一提的是,在分摊分析的时候,我们为了避免这样的情况,将分摊时间记为A,其等于实际时间T与势能差delta的和。其中势能可以理解为“银行”,简单操作省下来的时间会“积德行善”地存入一些多余的时间,在遇到最坏情况时我们再将这些“存款”取出,用于弥补不足。如是便能均衡地“劫富济贫”,完成分析。每一步的A之和不大于每一步的T之和,而每一步的A均不超过log n(当T为θ(n)时,势能函数会为一个θ(n)级别的负数)。具体过程请见邓公编写的习题解析8-2。
对于长度为n的文本串和长度为m的模式串,KMP算法的时间复杂度为:
O(n)。假如我们粗略地估计时间复杂度,大概率得出的结论是O(m*n)…然而假如我们记录一个观察值k=2 i - j,那么我们会发现无论是失败匹配还是成功匹配,其都会使得观察值k严格递增(至少加1),于是迭代过程至多不会超过2 n次,即时间复杂度为O(n)。(说是O(m+n)也行)
有2015个节点的左式堆,左子堆的规模最小为?
1。事实上正如教材所说,左式堆的左子堆未必要比右子堆“大”很多,左子堆的规模和高度都不一定大于其兄弟,甚至可以夸张到本题的程度。本题的例子是根的左子堆只有一个节点,右子堆根节点只有左孩子,其左孩子亦只有左孩子…即每个节点的右侧链都只有其本身,这样每个节点的npl均等于其右侧链长度1。
与MAD相比,除余法的缺陷在于:
不动点和高阶均匀性(相关性)。不动点是指hash(0)=0;高阶均匀性指相邻的关键码的地址一定相邻。而multipy-add-divide方法便不会有这些问题。
将1、2、3…2018插入到一个空伸展树中,若最终树高为2017,则插入的次序一定是单调的。
错误。比如1,2,3,4,6,5,7【5和6是乱序的!】,由于在7插入的时候会重新将splay tree变成单链,故诸如此类的操作仍然会形成单链。
linearselect最坏复杂度为?
O(n)。事实上,见教材 P 1274,我们取一堆小子序列中位数的中位数,以此作为轴点来解决轴点选取过差的问题。(此时轴点至少能排除n/4长度的差区间)我们得出如下公式:T(n)= c n+ T(n/Q) + T(3/(4 n))。
图的广度优先搜索访问各顶点的模式类似于二叉树的:
层次遍历。顺便一说,深度优先搜索类似于先序遍历。
多叉堆比二叉堆的操作复杂度更高?
错误。事实上,上滤成本会降低,而(由于至多需要比对d个孩子)下滤成本会升高。另一方面,d最好是2的次幂,否则不能直接借助移位操作来加快秩的计算。
在理想随机下,quickselect(k-select)的复杂度及其证明?
O(n)。我们记T(n)为期望比较次数,T(n) <= (n-1) + (2/n)*( T(2/n) + T(1+2/n) + … + T(n-1) ),在此我们大胆猜测T(n)< 4 n,归纳证明该结论是正确的。【“大胆猜想”,看来邓公数竞学的不错】
下图是一个三叉树实现的trie树,请写出其中储存的所有单词:
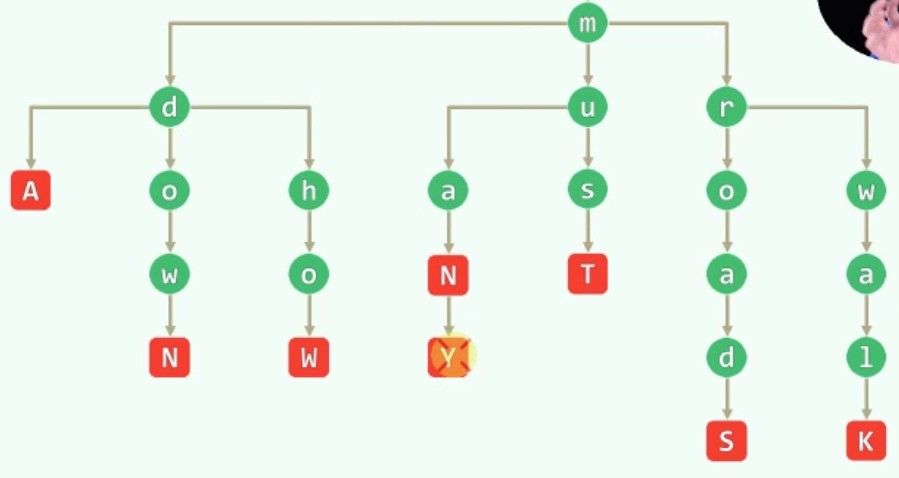
(顺序无关)how many roads must a man walk down.
三叉trie树的左右孩子都是“另开炉灶”的,只有中孩子继承了父亲的字母,比如中间的must,u是m的中孩子,s是u的中孩子,t是u的中孩子,故而有must。而d是m的左孩子,故而d没有继承m,该单词为down而非mdown。
在散列表中,一个好的散列函数h需要是单射?
错误。事实上不可能是单射,因为可用地址空间比所有词条的空间要小,所以一定会有多个词条映射到同一个地址。
若某算法的时间复杂度递归式可写为T(n)=2020 * T(n^(1/2020)) + O(log n),求其渐进复杂度。
log n* log log n。本题的递归式不是主定理传统的T(n/b),故而看起来我们对其无可奈何;但假如我们设m = log n,那么原式变成T(n) =R(m) = 2020 * R(m/2020) + O(m),故而得出结论。【这道题好像是OI的题吧?实在有点奇技淫巧】
请证明,如果表长为4k+3的素数,那么双向平方试探的确可以遍历所有地址空间。
首先,我们需要引入费马双平方引理及其推论,即一个自然数是两个整数的平方和当且仅当其4k+3形式的素因子的次数为偶数。如45=5*3^2,其等于9+36。
我们首先易得,正向试探中0 – 2k+1的模是互异的,而2k+2 – 4k+3与其完全对称。简单来说,n^2-m^2能被该素数整除当且仅当n+m等于该素数。
然后我们证明,反向试探中0 – 2k+1(同上,是互异的)与正向试探除了0之外,模都是互异的。否则,n^2+m^2可以被该素数整除,但由费马双平方引理知其只能整除该素数的平方、四次方…而这显然是不可能的,因为n^2+m^2小于该素数平方。
由此证毕,正向试探共有2k+2个(算上0),而反向试探共有2k+1个。
基于比较的排序算法,对于任何输入序列都需要至少Ω(n log n)时间。
错误。插入排序是输入敏感的,其最好情况只需O(n)时间。
在二叉树的先序、中序、后序遍历中,叶子节点的次序都是一样的。
正确。这是一个蛮有意思的小结论。
基于二分查询A版本改进的fib查找,对于长度为n=fib(k)-1的向量,最坏查找长度为?
k-1。可以用归纳证明:由于fib(k)-1左右区间分别为fib(k-1)-1和fib(k-2)-1,向左的最坏长度为k-2+1,向右的最坏长度为k-3+2,均为k-1。本题也体现了最坏情况下fib查找的均衡性。
具有2020个内部节点的红黑树的最大黑高度是?
10。黑高度=其等价B树的高度。另一方面,最大高度有些困难,我们试图让一个红黑树的高度等于其黑高度的二倍,并且用尽可能少的节点,故而我们只用h/2个红色节点即可。后续计算相对麻烦,详见习题解析8-13。
请证明:高度为h的AVL树,其叶子节点的深度不会小于h/2向上取整。
对h做归纳(h=1时显然)。假设以上命题对高度小于h的AVL 树均成立,以下考查高度为h的AVL树:
由于左、右子树的高度至多为h - 1,至少为h - 2,由归纳假设,高度h-1的叶子节点到该子树根的深度至少为(h-1)/2向上取整,大于等于h/2向上取整 -1;高度h-1的叶子节点到该子树根的深度至少为h/2向上取整 -1。故而无论是h-1还是h-2,其叶子到总根节点的深度均不小于h/2向上取整 -1 +1。证毕。
本题体现了归纳法在树状结构(顺便一说,二分查找这类的证明题也可视作类树)中的出色发挥
若将众数的定义改为“一半及一半以上的元素同为m,则m为众数”(原定义为:一半以上的元素同为m),课本P 1258的majCandidate算法是否还正确?
错误。虽然对于向量长度为奇数时,修改的定义显然与原定义没有区别,但对于向量长度为偶数时,我们很容易便能举出反例:0, 0, 0, 0, 1, 1, 1, 1, 2, 1。其中1是我修改定义后的众数,但算法会认为2是众数的候选者。本例中我们也能看到,算法选取的众数候选者甚至有可能是一个仅出现过一次的龙套元素。
若T(n)=O(n^2),F(n)=O(n),则T(n)/F(n)=O(n^2)。
错误。事实上复杂度函数可以小于常数如F(n)=θ(1/n),对于本课程而言请注意这种可能性的存在。【虽然但是,小于常数有什么意义?反正背就完了】
在中缀表达式求值的时候,优先级表中有对应了非法表达式的空格项,列出所有这样的栈顶/当前运算符组合。
“(“与”\0”、”)”与所有运算符、”\0”与”)”、”!”与”(“(其中第一个为栈顶运算符,第二个为当前运算符)。即左括号不可能留到最后而不遇到右括号;右括号不可能进入运算符栈;!是单目运算符,不可能直接与左括号相邻。
为了实现”在2014个元素中挑选5个最大元素“的功能,在最坏情况下锦标赛树和二叉堆的比较次数相同吗?
不相同,后者是前者的二倍。与简单的上滤不同,每一步下滤需要和左右孩子都比较一番,而锦标赛树只需比较一次即可。
规模为n的任何两棵等价二叉搜索树,至多经过2n - 2 次旋转调整,即可彼此转换。
正确。见习题解析7-15,将任意一棵”最左侧通路“长为s的(博主个人认为这东西几乎就是相对于npl右侧链的左侧链)二叉搜索树转换为一个左倾单链需要n-1-s步旋转。故而可知我们可以将树A先转为单链,再将单链反向转为树B,至多不会超过2n-2次旋转。
对不含括号的中缀表达式求值时,操作符栈的容量可以固定为某一常数。
正确。对于优先级表中除了左右括号和结束符/0之外的操作符,当栈顶和当前运算符均为此操作符时,优先级均为栈顶>当前,故而在不存在括号的情况下,操作符栈不可能堆叠大量运算符;在堆叠了各种不同的操作符后一定会执行运算并开始清除栈中元素。
带权重的最优PFC(前缀无歧义)编码树不仅未必唯一、拓扑结构未必相同,甚至树高也可能不等。
正确。对于Huffman算法,若有出现频率相同的字符(或是在合并过程中存在出现频率相同的子树),则会有歧义的发生,这样的歧义虽不会导致Huffman树的最优性,却会导致不同结构的情况,这就是所谓Huffman树的不唯一性(另两个性质是内部节点的双子性和层次性)。至于题中所说的情况,abcd的出现频率分别是2211,这个简单的例子就可以构造出两棵高度不同的Huffman树。
考后感想
妈的,设计大题让设计一个括号匹配的数据结构。不会做,二十分白给,寄。
印象很深的两道题目是“指出教材中【为了易于理解而牺牲效率】的两个算法”和设计答题“请设计一个有插入功能的左右括号匹配判别器”(具体需求复杂度忘了,据说是用二叉树+lazy标记解决)。这两道题博主没有做出来…
可能是因为判断题和简答题做的还不错(不过简答题第一题就不会,问的是教材中有些算法为了精简代码而牺牲了效率,根本没记)最后还是拿A-了,邓公太善良了T T
2023年秋季的反馈
据说2023年秋考了不少具体算法的题目(比如那个求最大矩形的算法)。看来考前复习一下邓公给的那些excel的demo是有必要的。




